Searching in a graph is the one of the most popular topic in CS.

In this article, I would like to make a summary about what algorithms for searching in graphes.

1. Presentation of Graph

  • Adjacency Matrix
  • Adjacency List

What is better, adjacency lists or adjacency matrices for graph problem ?

It depends on the problem.

An adjacency matrix uses O(n*n) memory. It has fast lookups to check for presence or absence of a specific edge, but slow to iterate over all edges.

Adjacency lists use memory in proportion to the number edges, which might save a lot of memory if the adjacency matrix is sparse. It is fast to iterate over all edges, but finding the presence or absence specific edge is slightly slower than with the matrix.

In this article, I would like to use adjacency matrix to represent the graph in our problems. I want to express the essential idea in algorithms but not the programming language grammer. So all implementation of algorithm will be written in Python.

We will try to use different ways to solve the demo problem. Here is the graph which we will use in this article.

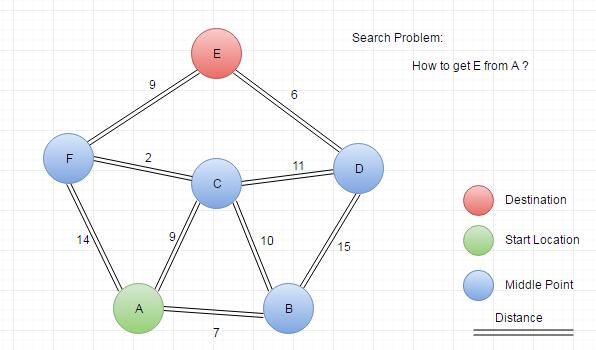
images

The corresponding adjacency matrix:

1
2
3
4
5
6
7
8
9
10
INF = float('inf')
graph = [
[INF,   7,   9, INF, INF,  14],
[  7, INF,  10,  15, INF, INF],
[  9,  19, INF,  11, INF,   2],
[INF,  15,  11, INF,   6, INF],
[INF, INF, INF,   6, INF,   9],
[ 14, INF,   2, INF,   9, INF]
]

Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key’) and explores the neighbor nodes first, before moving to the next level neighbors.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def BFS(matrix, start, end):
    size = len(matrix)
    visited = [start]
    Q = [ [start] ]
    path = [] # possible solution, @path is a nested list [[] ...]
    while len(Q) != 0:
        path = Q.pop(0)
        curNode = path[-1]
        if curNode == end:
            return path # the solution
        neighbors = []
        for i in xrange(size):
            if matrix[curNode][i] != INF:
            neighbors.append(i)
        # to find the neighbors who are unvisited
        i = 0
        while i < len(neighbors):
            if neighbors[i] in visited:
                neighbors.remove(neighbors[i])
            else:
                i += 1
        #add unvisited neighbor into visited line.
        for i in neighbors:
            visited.append(i)
            Q.append(path + [i])
    return None

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. One starts at the root (selecting some arbitrary node as the root in the case of a graph) and explores as far as possible along each branch before backtracking.

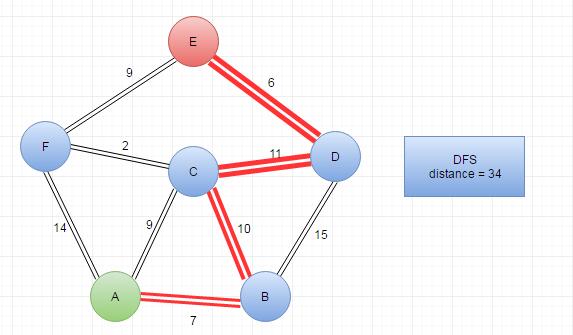
images

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#####################  Pesudo Code ########################
Input: A graph G and a vertex v of G
Output: All vertices reachable from v labeled as discovered
-----------------------------------------------------------
A recursive implementation of DFS:
-----------------------------------------------------------
procedure DFS(G,v):
    label v as discovered
    for all edges from v to w in G.adjacentEdges(v) do
        if vertex w is not labeled as discovered then
            recursively call DFS(G,w)
------------------------------------------------------------
A non-recursive implementation of DFS:
------------------------------------------------------------
procedure DFS-iterative(G,v):
    let S be a stack
    S.push(v)
    while S is not empty
        v = S.pop()
        if v is not labeled as discovered:
            label v as discovered
            for all edges from v to w in G.adjacentEdges(v) do
                 S.push(w)

Foly

Shortest Path Search (Dijkastra)

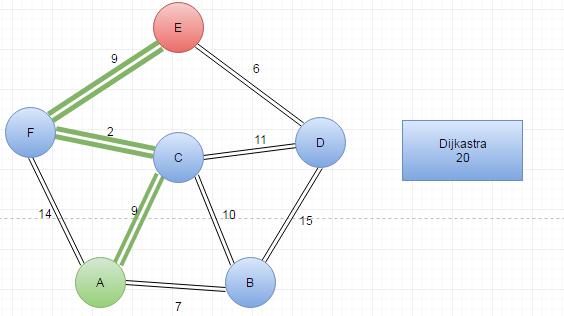
images

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#####################  Pesudo Code ########################
function Dijkstra(Graph, source):
      create vertex set Q
      for each vertex v in Graph:             // Initialization
          dist[v] ← INFINITY                  // Unknown distance from source to v
          prev[v] ← UNDEFINED                 // Previous node in optimal path from source
          add v to Q                          // All nodes initially in Q (unvisited nodes)
      dist[source] ← 0                        // Distance from source to source
      
      while Q is not empty:
          u ← vertex in Q with min dist[u]    // Source node will be selected first
          remove u from Q 
          
          for each neighbor v of u:           // where v is still in Q.
              alt ← dist[u] + length(u, v)
              if alt < dist[v]:               // A shorter path to v has been found
                  dist[v] ← alt 
                  prev[v] ← u 
      return dist[], prev[]

Extention:

I will recommend you to finish the lab2 in 6.034

https://github.com/jasonleaster/MIT_6.034_2015/tree/master/lab2

This article does not finished and will be update these days :)

You can get my implementation on github

Photo by Annabella in ChongQin, China
images